Чому дорівнює діагональ квадрата: глибокий аналіз та приклади
Питання “чому дорівнює діагональ квадрата” зазвичай виникає під час вивчення геометрії та аналітичної геометрії. Діагональ квадрата є базовою концепцією, але вона також пов’язана з багатьма іншими геометричними та алгебраїчними поняттями, які варто досліджувати. У цьому матеріалі ми дамо детальний огляд, як розрахувати діагональ квадрата, використовуючи різні методи та теореми, а також розглянемо її застосування в реальному світі.
Що таке квадрат і його основні властивості
Перед тим, як обговорювати діагональ квадрата, важливо зрозуміти, що таке квадрат і які його основні властивості. Квадрат — це геометрична фігура, яка має чотири рівні сторони і чотири прямі кути (по 90 градусів кожен).
Властивості квадрата:
- Усі сторони квадрата рівні.
- Усі кути квадрата є прямими.
- Діагоналі квадрата рівні за довжиною.
- Діагоналі квадрата перетинаються під прямим кутом.
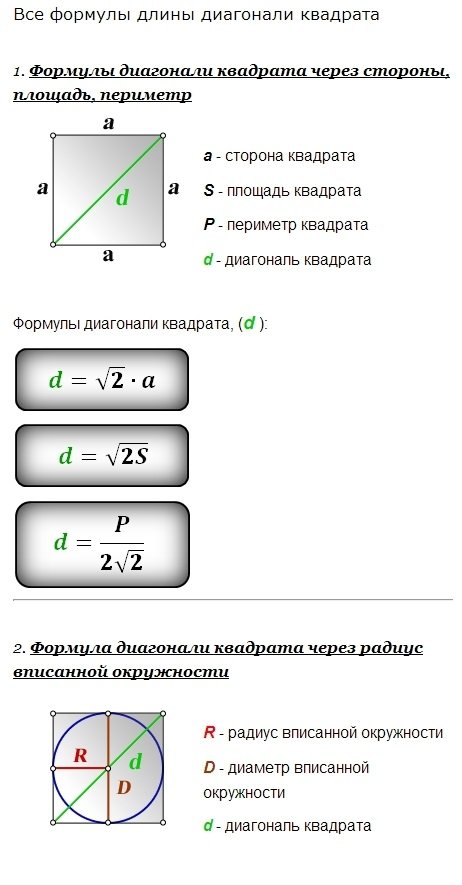
Формула діагоналі квадрата
Як знайти діагональ квадрата? Це запитання має просте рішення через застосування теореми Піфагора. Візьмемо квадрат зі стороною a. Розглянемо один його трикутник: він буде прямокутним, адже квадрат, як ми вже зазначили, має прямі кути.
Піфагорова теорема:
Для будь-якого прямокутного трикутника з катетами a і b, і гіпотенузою c, виконується формула:
c2 = a2 + b2
Оскільки у квадрата всі сторони рівні, то в нашому випадку:
d2 = a2 + a2 = 2a2
Тобто:
d = a√2
Цю формулу часто використовують у задачах з геометрії для обчислення довжини діагоналі квадрата. Формула показує, що довжина діагоналі квадрата є твірною сторони квадрата на корінь з двох.
Практичне застосування формули в задачах
Давайте розглянемо практичні приклади, щоб краще зрозуміти, чому дорівнює діагональ квадрата. Використаємо формулу d = a√2 для розв’язування задачі.
- Умова: Дано квадрат зі стороною 5 см. Знайти діагональ квадрата.
- Рішення:
- Використовуємо формулу: d = a√2.
- Підставляємо значення: d = 5√2.
- Обчислюємо: d ≈ 5 * 1.414 = 7.07 см.
Таким чином, ми знайшли, що діагональ квадрата зі стороною 5 см дорівнює приблизно 7,07 см.
Діагональ квадрата в різних математичних системах
Важливо зазначити, що таке, здавалося б, просте поняття, як діагональ квадрата, може бути розглянуто з точки зору різних математичних систем.
Картизіанська система координат
У системі координат XY, квадрат може бути представлений як сукупність точок, наприклад A(0,0), B(a,0), C(a,a), і D(0,a). Діагональ тут можна знайти через формулу відстані між точками:
| Точка | Координата |
|---|---|
| A | (0,0) |
| C | (a,a) |
Відстань AC обчислюємо за аплікацією:
d = √((a - 0)2 + (a - 0)2) = √(a2 + a2) = a√2
Таким чином, ми ще раз підтверджуємо, чому дорівнює діагональ квадрата.
Висновки
Діагональ квадрата відіграє важливу роль у геометрії. Знаючи, чому дорівнює діагональ квадрата, ми можемо вирішити різноманітні задачі, починаючи від простих розрахунків площі та периметра й завершуючи оптимізацією складних систем. Використання основних геометричних формул та розуміння властивостей геометричних фігур допомагає не лише в академічних розрахунках, але й у повсякденному житті.
Ця тема демонструє красу і простоту геометрії та її незамінність у широкому спектрі практичних застосувань.